30 Discussion 02: CSPs (From Spring 2025)
Slides
30.1 CSPs: Trapped Pacman
Pacman is trapped! He is surrounded by mysterious corridors, each of which leads to either a pit (P), a ghost (G), or an exit (E). In order to escape, he needs to figure out which corridors, if any, lead to an exit and freedom, rather than the certain doom of a pit or a ghost.
The one sign of what lies behind the corridors is the wind: a pit produces a strong breeze (S) and an exit produces a weak breeze (W), while a ghost doesn’t produce any breeze at all. Unfortunately, Pacman cannot measure the strength of the breeze at a specific corridor. Instead, he can stand between two adjacent corridors and feel the max of the two breezes. For example, if he stands between a pit and an exit he will sense a strong (S) breeze, while if he stands between an exit and a ghost, he will sense a weak (W) breeze. The measurements for all intersections are shown in the figure below.
Also, while the total number of exits might be zero, one, or more, Pacman knows that two neighboring squares will not both be exits.
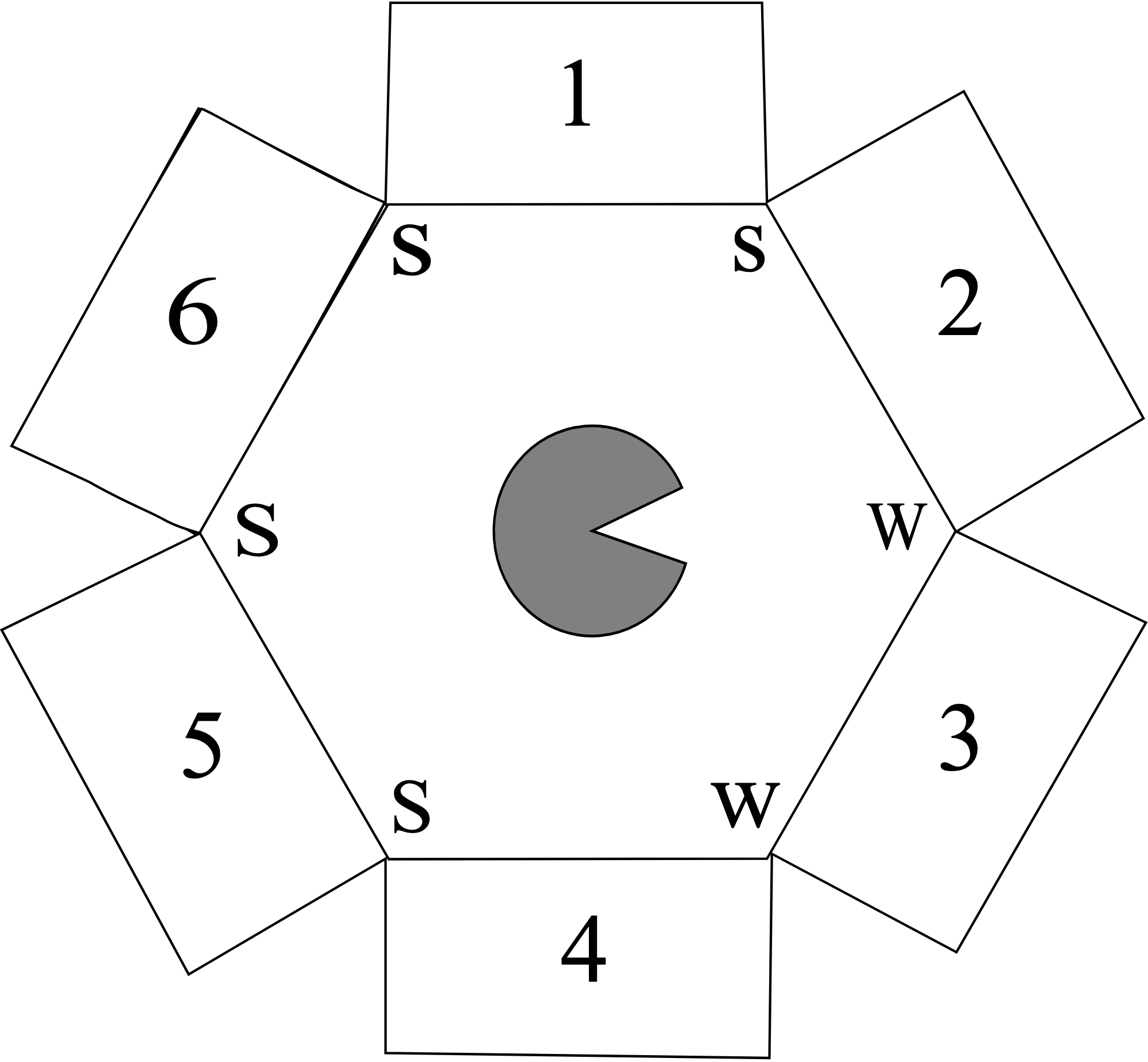
Pacman models this problem using variables \(X_i\) for each corridor \(i\) and domains P, G, and E.
30.1.1 (a)
State the binary and/or unary constraints for this CSP (either implicitly or explicitly).
Answer
\[ \text{Binary:} \quad \begin{array}{l l } X_1 = P \text{ or } X_2 = P, & X_2 = E \text{ or } X_3 = E, \\ X_3 = E \text{ or } X_4 = E, & X_4 = P \text{ or } X_5 = P, \\ X_5 = P \text{ or } X_6 = P, & X_1 = P \text{ or } X_6 = P, \\ \text{For all } i,j \text{ s.t. Adj}(i,j): \neg (X_i = E \text{ and } X_j = E) & \end{array} \] \[ \text{Unary:} \quad \begin{cases} X_2 \ne P,\\ X_3 \ne P,\\ X_4 \ne P \end{cases} \]
Note: This is just one of many solutions. The answers below will be based on this formulation.30.1.2 (b)
Suppose we assign \(X_1\) to \(E\). Perform forward checking after this assignment. Also, enforce unary constraints.
\[ \begin{array}{|l|c|c|c|} \hline X_1 & \text{ } & \text{ } & E \\ \hline X_2 & P & G & E \\ \hline X_3 & P & G & E \\ \hline X_4 & P & G & E \\ \hline X_5 & P & G & E \\ \hline X_6 & P & G & E \\ \hline \end{array} \]
Answer
\[ \begin{array}{|l|c|c|c|} \hline X_1 & \text{ } & \text{ } & E \\ \hline X_2 & \text{ } & \text{ } & \text{ } \\ \hline X_3 & \text{ } & G & E \\ \hline X_4 & \text{ } & G & E \\ \hline X_5 & P & G & E \\ \hline X_6 & P & \text{ } & \text{ } \\ \hline \end{array} \]
30.1.3 (c)
Suppose forward checking returns the following set of possible assignments:
\[ \begin{array}{|l|c|c|c|} \hline X_1 & P & & \\ \hline X_2 & & G & E \\ \hline X_3 & & G & E \\ \hline X_4 & & G & E \\ \hline X_5 & P & & \\ \hline X_6 & P & G & E \\ \hline \end{array} \]
According to MRV, which variable or variables could the solver assign first?
Answer
\(X_1\) or \(X_5\) (tie breaking)30.1.4 (d)
Assume that Pacman knows that \(X_6=G\). List all the solutions of this CSP or write none if no solutions exist.
Answer
(P,E,G,E,P,G)(P,G,E,G,P,G)
30.2 Course Scheduling
You are in charge of scheduling for computer science classes that meet Mondays, Wednesdays and Fridays. There are 5 classes that meet on these days and 3 professors who will be teaching these classes. You are constrained by the fact that each professor can only teach one class at a time.
The classes are:
- Class 1 - Intro to Programming: meets from 8:00-9:00am
- Class 2 - Intro to Artificial Intelligence: meets from 8:30-9:30am
- Class 3 - Natural Language Processing: meets from 9:00-10:00am
- Class 4 - Computer Vision: meets from 9:00-10:00am
- Class 5 - Machine Learning: meets from 10:30-11:30am
The professors are:
- Professor A, who is qualified to teach Classes 1, 2, and 5.
- Professor B, who is qualified to teach Classes 3, 4, and 5.
- Professor C, who is qualified to teach Classes 1, 3, and 4.
30.2.1 (a)
Formulate this problem as a CSP problem in which there is one variable per class, stating the domains (after enforcing unary constraints), and binary constraints. Constraints should be specified formally and precisely, but may be implicit rather than explicit.
Answer
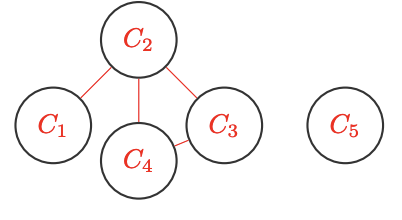
\[ \begin{array}{rl} \text{Variables} & \text{Domains (or unary constraints)} \\ C_1 & \{A, C\} \\ C_2 & \{A\} \\ C_3 & \{B, C\} \\ C_4 & \{B, C\} \\ C_5 & \{A, B\} \end{array} \]
\[ \begin{array}{l} \text{Binary Constraints} \\ C_1 \ne C_2 \\ C_2 \ne C_3 \\ C_2 \ne C_4 \\ C_3 \ne C_4 \end{array} \]
30.2.2 (b)
Draw the constraint graph associated with your CSP.
Answer