32 Discussion 04: MDPs (From Spring 2025)
Slides
32.1 MDPs: Micro-Blackjack
In micro-blackjack, you repeatedly draw a card (with replacement) that is equally likely to be a 2, 3, or 4. You can either Draw or Stop if the total score of the cards you have drawn is less than 6. If your total score is 6 or higher, the game ends, and you receive a utility of 0. When you Stop, your utility is equal to your total score (up to 5), and the game ends. When you Draw, you receive no utility. There is no discount (\(\gamma = 1\)). Let’s formulate this problem as an MDP with the following states: \(0, 2, 3, 4, 5\) and a \(Done\) state, for when the game ends.
32.1.1 (a)
What is the transition function and the reward function for this MDP?
Answer
\[ \begin{aligned} T(s, \text{Stop}, \text{Done}) &= 1 \\ T(0, \text{Draw}, s') &= \frac{1}{3}, \quad s' \in \{2, 3, 4\} \\ T(2, \text{Draw}, s') &= \frac{1}{3}, \quad s' \in \{4, 5, \text{Done}\} \\ T(3, \text{Draw}, s') &= \begin{cases} \frac{1}{3}, & s' = 5 \\ \frac{2}{3}, & s' = \text{Done} \end{cases} \\ T(4, \text{Draw}, \text{Done}) &= 1 \\ T(5, \text{Draw}, \text{Done}) &= 1 \\ T(s, a, s') &= 0, \quad \text{otherwise} \end{aligned} \]
The reward function is
\[ R(s, \text{Stop}, \text{Done}) = s, \quad s \le 5 \]
\[ R(s, a, s') = 0, \quad \text{otherwise} \]32.1.2 (b)
Fill in the following table of value iteration values for the first 4 iterations.
\[ \begin{array}{|c|c|c|c|c|c|} \hline \text{States} & 0 & 2 & 3 & 4 & 5 \\ \hline V_0 & \text{ } & \text{ } & \text{ } & \text{ } & \text{ } \\ \hline V_1 & \text{ } & \text{ } & \text{ } & \text{ } & \text{ } \\ \hline V_2 & \text{ } & \text{ } & \text{ } & \text{ } & \text{ } \\ \hline V_3 & \text{ } & \text{ } & \text{ } & \text{ } & \text{ } \\ \hline V_4 & \text{ } & \text{ } & \text{ } & \text{ } & \text{ } \\ \hline \end{array} \]
Answer
\[ \begin{array}{|c|c|c|c|c|c|} \hline \text{States} & 0 & 2 & 3 & 4 & 5 \\ \hline V_0 & 0 & 0 & 0 & 0 & 0 \\ \hline V_1 & 0 & 2 & 3 & 4 & 5 \\ \hline V_2 & 3 & 3 & 3 & 4 & 5 \\ \hline V_3 & 10/3 & 3 & 3 & 4 & 5 \\ \hline V_4 & 10/3 & 3 & 3 & 4 & 5 \\ \hline \end{array} \]
32.1.3 (c)
You should have noticed that value iteration converged above. What is the optimal policy for the MDP? \[ \begin{array}{|c|c|c|c|c|c|} \hline \text{States} & 0 & 2 & 3 & 4 & 5 \\ \hline \pi^* & \text{ } & \text{ } & \text{ } & \text{ } & \text{ } \\ \hline \end{array} \]
Answer
\[ \begin{array}{|c|c|c|c|c|c|} \hline \text{States} & 0 & 2 & 3 & 4 & 5 \\ \hline \pi^* & \text{Draw} & \text{Draw} & \text{Stop} & \text{Stop} & \text{Stop} \\ \hline \end{array} \]
32.1.4 (d)
Perform one iteration of policy iteration for one step of this MDP, starting from the fixed policy below:
\[ \begin{array}{|c|c|c|c|c|c|} \hline \text{States} & 0 & 2 & 3 & 4 & 5 \\ \hline \pi_i & \text{Draw} & \text{Stop} & \text{Draw} & \text{Stop} & \text{Draw} \\ \hline V^{\pi_i} & \textbf{ } & \textbf{ } & \textbf{ } & \textbf{ } & \textbf{ } \\ \hline \pi_{i+1} & \text{ } & \text{ } & \text{ } & \text{ } & \text{ } \\ \hline \end{array} \]
Answer
\[ \begin{array}{|c|c|c|c|c|c|} \hline \text{States} & 0 & 2 & 3 & 4 & 5 \\ \hline \pi_i & \text{Draw} & \text{Stop} & \text{Draw} & \text{Stop} & \text{Draw} \\ \hline V^{\pi_i} & 2 & 2 & 0 & 4 & 0 \\ \hline \pi_{i+1} & \text{Draw} & \text{Stop} & \text{Stop} & \text{Stop} & \text{Stop} \\ \hline \end{array} \]
32.2 MDPs: Grid-World Water Park
Consider the MDP drawn below. The state space consists of all squares in a grid-world water park. There is a single waterslide that is composed of two ladder squares and two slide squares (marked with vertical bars and squiggly lines respectively). An agent in this water park can move from any square to any neighboring square, unless the current square is a slide in which case it must move forward one square along the slide. The actions are denoted by arrows between squares on the map and all deterministically move the agent in the given direction. The agent cannot stand still: it must move on each time step. Rewards are also shown below: the agent feels great pleasure as it slides down the water slide (+2), a certain amount of discomfort as it climbs the rungs of the ladder (-1), and receives rewards of 0 otherwise. The time horizon is infinite; this MDP goes on forever.
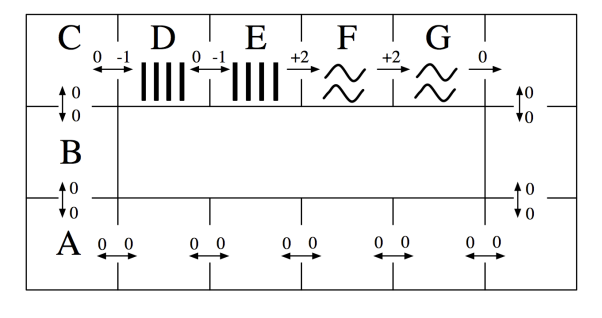
32.2.1 (a)
How many (deterministic) policies \(\pi\) are possible for this MDP?
Answer
\(2^{11}\)32.2.2 (b)
Fill in the blank cells of this table with values that are correct for the corresponding function, discount, and state. Hint: You should not need to do substantial calculation here. (Note: \(V_t(s)\) is the time-limited value of state \(s\), if our Markov Decision Process were to terminate after \(t\) timesteps.)
| \(\gamma\) | \(s=A\) | \(s=E\) | |
|---|---|---|---|
| \(V_3(s)\) | 1.0 | ||
| \(V_{10}(s)\) | 1.0 | ||
| \(V_{10}(s)\) | 0.1 | ||
| \(Q_1(s, \text{west})\) | 1.0 | — | |
| \(Q_{10}(s, \text{west})\) | 1.0 | — | |
| \(V^*(s)\) | 1.0 | ||
| \(V^*(s)\) | 0.1 |
Answer
| \(\gamma\) | \(s=A\) | \(s=E\) | |
|---|---|---|---|
| \(V_3(s)\) | 1.0 | 0 | 4 |
| \(V_{10}(s)\) | 1.0 | 2 | 4 |
| \(V_{10}(s)\) | 0.1 | 0 | 2.2 |
| \(Q_1(s, \text{west})\) | 1.0 | — | 0 |
| \(Q_{10}(s, \text{west})\) | 1.0 | — | 3 |
| \(V^*(s)\) | 1.0 | \(\infty\) | \(\infty\) |
| \(V^*(s)\) | 0.1 | 0 | 2.2 |
\(V_{10}(A), \gamma = 1\): No discounting, the rewards don’t decay, so the optimal strategy is to climb the two stairs (-1 reward each), and then slide down the two slide squares (+2 rewards each). You only have time to do this once. Summing this up, we get \(-1 - 1 + 2 + 2 = 2\).
\(V_{10}(E), \gamma = 1\): No discounting, so optimal strategy is sliding down the slide. That’s all you have time for. Sum of rewards \(= 2 + 2 = 4\).
\(V_{10}(A), \gamma = 0.1\): The discount rate is 0.1, meaning that rewards 1 step further into the future are discounted by a factor of 0.1. Let’s assume from A we went for the slide. Then, we would have to take the actions \(A \rightarrow B, B \rightarrow C, C \rightarrow D, D \rightarrow E, E \rightarrow F, F \rightarrow G\). We get the first -1 reward from \(C \rightarrow D\), discounted by \(\gamma^2\) since it is two actions in the future. \(D \rightarrow E\) is discounted by \(\gamma^3\), \(E \rightarrow F\) by \(\gamma^4\), and \(F \rightarrow G\) by \(\gamma^5\). Since \(\gamma\) is low, the positive rewards you get from the slide have less of an effect as the larger negative rewards you get from climbing up. Hence, the sum of rewards of taking the slide path would be negative; the optimal value is 0.
\(V_{10}(E), \gamma = 0.1\): Now, you don’t have to do the work of climbing up the stairs, and you just take the slide down. Sum of rewards would be \(2\) (for \(E \rightarrow F\)) + \(0.2\) (for \(F \rightarrow G\), discounted by \(0.1) = 2.2\).
\(Q_{10}(E, \text{west}), \gamma = 1\): Remember that a Q-state \((s,a)\) is when you start from state \(s\) and are committed to taking action \(a\). Hence, from E, you take the action West and land in D, using up one time step and getting an immediate reward of 0. From D, the optimal strategy is to climb back up the higher flight of stairs and then slide down the slide. Hence, the rewards would be \(-1(D \rightarrow E) + 2(E \rightarrow F) + 2(F \rightarrow G) = 3\).
\(V^*(s), \gamma = 1\): Infinite game with no discount? Have fun sliding down the slide to your content from anywhere.
\(V^*(s), \gamma = 0.1\): Same reasoning apply to both A and E from \(V_{10}(s)\). With discounting, the stairs are more costly to climb than the reward you get from sliding down the water slide. Hence, at A, you wouldn’t want to head to the slide. From E, since you are already at the top of the slide, you should just slide down.32.2.3 (c)
Fill in the blank cells of this table with the Q-values that result from applying the Q-update for the transition specified on each row. You may leave Q-values that are unaffected by the current update blank. Use discount \(\gamma\) = 1.0 and learning rate \(\alpha\) = 0.5. Assume all Q-values are initialized to 0. (Note: the specified transitions would not arise from a single episode.)
| \(Q(D, \text{west})\) | \(Q(D, \text{east})\) | \(Q(E, \text{west})\) | \(Q(E, \text{east})\) | |
|---|---|---|---|---|
| Initial | 0 | 0 | 0 | 0 |
| Transition 1: (\(s=D, a=\text{east}, r=-1, s'=E\)) | ||||
| Transition 2: (\(s=E, a=\text{east}, r=+2, s'=F\)) | ||||
| Transition 3: (\(s=E, a=\text{west}, r=0, s'=D\)) | ||||
| Transition 4: (\(s=D, a=\text{east}, r=-1, s'=E\)) |
Answer
| \(Q(D, \text{west})\) | \(Q(D, \text{east})\) | \(Q(E, \text{west})\) | \(Q(E, \text{east})\) | |
|---|---|---|---|---|
| Initial | 0 | 0 | 0 | 0 |
| Transition 1: (\(s=D, a=\text{east}, r=-1, s'=E\)) | -0.5 | |||
| Transition 2: (\(s=E, a=\text{east}, r=+2, s'=F\)) | 1.0 | |||
| Transition 3: (\(s=E, a=\text{west}, r=0, s'=D\)) | ||||
| Transition 4: (\(s=D, a=\text{east}, r=-1, s'=E\)) | 0.25 |
