31 Discussion 03: Game Trees (From Spring 2025)
Slides
31.1 Games
31.1.1 (a)
Consider the zero-sum game tree shown below. Triangles that point up, such as at the top node (root), represent choices for the maximizing player; triangles that point down represent choices for the minimizing player. Assuming both players act optimally, fill in the minimax value of each node.

Answer
See part (b).31.1.2 (b)
Which nodes can be pruned from the game tree above through alpha-beta pruning? If no nodes can be pruned, explain why not. Assume the search goes from left to right; when choosing which child to visit first, choose the left-most unvisited child.
Answer
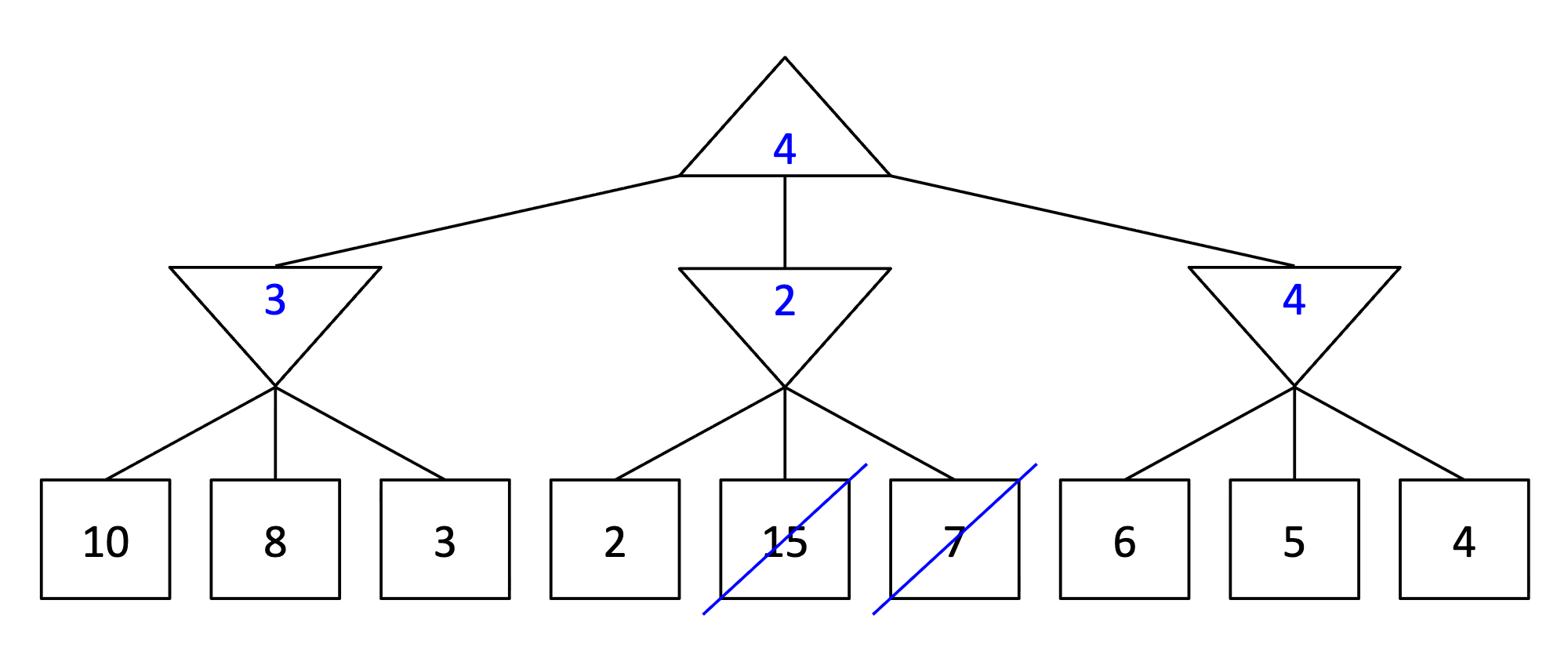
31.1.3 (c)
Again, consider the same zero-sum game tree, except that now, instead of a minimizing player, we have a chance node that will select one of the three values uniformly at random. Fill in the expectimax value of each node. The game tree is redrawn below for your convenience.

Answer
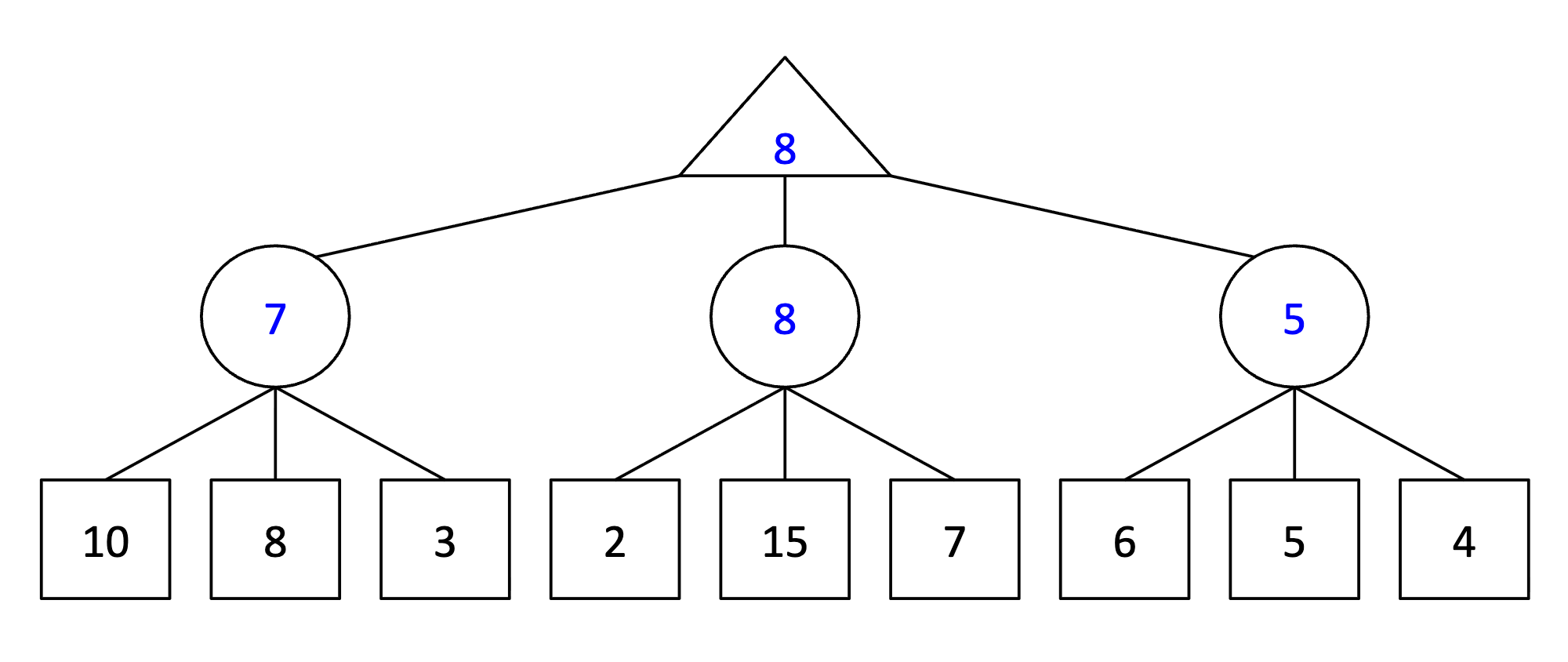
31.1.4 (d)
Which nodes can be pruned from the game tree above through alpha-beta pruning? If no nodes can be pruned, explain why not.
Answer
No nodes can be pruned. There will always be the possibility that an as-yet-unvisited leaf of the current parent chance node will have a very high value, which increases the overall average value for that chance node. For example, when we see that leaf 4 has a value of 2, which is much less than the value of the left chance node, 7, at this point we cannot make any assumptions about how the value of the middle chance node will ultimately be more or less in value than the left chance node. As it turns out, the leaf 5 has a value of 15, which brings the expected value of the middle chance node to 8, which is greater than the value of the left chance node. In the case where there is an upper bound to the value of a leaf node, there is a possibility of pruning: suppose that an upper bound of +10 applies only to the children of the rightmost chance node. In this case, after seeing that leaf 7 has a value of 6 and leaf 8 has a value of 5, the best possible value that the rightmost chance node can take on is \(\frac{6+5+10}{3}=7\), which is less than 8, the value of the middle chance node. Therefore, it is possible to prune leaf 9 in this case.31.2 Nonzero-sum Games
31.2.1 (a)
Let’s look at a non-zero-sum version of a game. In this formulation, player A’s utility will be represented as the first of the two leaf numbers, and player B’s utility will be represented as the second of the two leaf numbers. Fill in this non-zero game tree assuming each player is acting optimally.

Answer
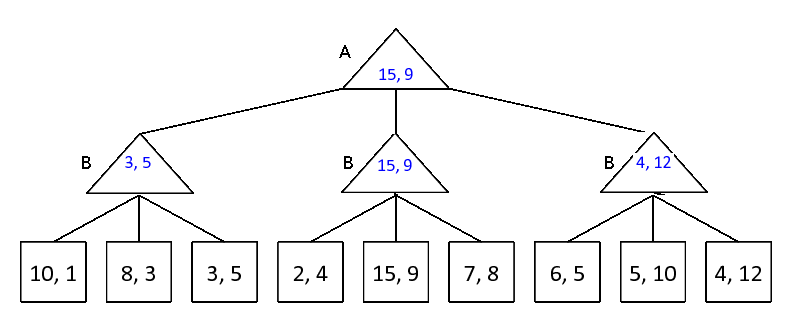
31.2.2 (b)
Which nodes can be pruned from the game tree above through alpha-beta pruning? If no nodes can be pruned, explain why not.
