36 Discussion 08: VPIs and HMMs (From Spring 2025)
Slides
36.1 HMMs
Consider the following Hidden Markov Model. \(O_1\) and \(O_2\) are supposed to be shaded.

| \(W_1\) | \(P(W_1)\) |
|---|---|
| 0 | 0.3 |
| 1 | 0.7 |
| \(W_t\) | \(W_{t+1}\) | \(P(W_{t+1}\mid W_t)\) |
|---|---|---|
| 0 | 0 | 0.4 |
| 0 | 1 | 0.6 |
| 1 | 0 | 0.8 |
| 1 | 1 | 0.2 |
| \(W_t\) | \(O_t\) | \(P(O_t\mid W_t)\) |
|---|---|---|
| 0 | a | 0.9 |
| 0 | b | 0.1 |
| 1 | a | 0.5 |
| 1 | b | 0.5 |
Suppose that we observe \(O_1 = a\) and \(O_2 = b\).
Using the forward algorithm, compute the probability distribution \(P(W_2 \mid O_1 = a, O_2 = b)\) one step at a time.
36.1.1 (a)
Compute \(P(W_1, O_1 = a)\)
Answer
\(P(W_1, O_1 = a) = P(W_1)P(O_1 = a \mid W_1)\)
\(P(W_1 = 0, O_1 = a) = (0.3)(0.9) = 0.27\)
\(P(W_1 = 1, O_1 = a) = (0.7)(0.5) = 0.35\)
36.1.2 (b)
Using the previous calculation, compute \(P(W_2, O_1 = a)\)
Answer
\(P(W_2, O_1 = a) = \sum_{w_1} P(w_1, O_1 = a)P(W_2 \mid w_1)\)
\(P(W_2 = 0, O_1 = a) = (0.27)(0.4) + (0.35)(0.8) = 0.388\)
\(P(W_2 = 1, O_1 = a) = (0.27)(0.6) + (0.35)(0.2) = 0.232\)
36.1.3 (c)
Using the previous calculation, compute \(P(W_2, O_1 = a, O_2 = b)\)
Answer
\(P(W_2, O_1 = a, O_2 = b) = P(W_2, O_1 = a)P(O_2 = b \mid W_2)\)
\(P(W_2 = 0, O_1 = a, O_2 = b) = (0.388)(0.1) = 0.0388\)
\(P(W_2 = 1, O_1 = a, O_2 = b) = (0.232)(0.5) = 0.116\)
36.1.4 (d)
Finally, compute \(P(W_2 \mid O_1 = a, O_2 = b)\)
Answer
Renormalizing the distribution above, we have:
\[ P(W_2 = 0 \mid O_1 = a, O_2 = b) = \frac{0.0388}{0.0388 + 0.116} \approx 0.25 \]
\[ P(W_2 = 1 \mid O_1 = a, O_2 = b) = \frac{0.116}{0.0388 + 0.116} \approx 0.75 \]
36.2 Decision Networks and VPI
Valerie has just found a cookie on the ground. She is concerned that the cookie contains raisins, which she really dislikes but she still wants to eat the cookie. If she eats the cookie and it contains raisins she will receive a utility of −100 and if the cookie doesn’t contain raisins she will receive a utility of 10. If she doesn’t eat the cookie she will get 0 utility. The cookie contains raisins with probability 0.1.
36.2.1 (a)
Should Valerie eat the cookie?
Answer
36.2.2 (b)
Valerie can now smell the cookie to judge whether it has raisins before she eats it. However, since she dislikes raisins she does not have much experience with them and cannot recognize their smell well. As a result she will incorrectly identify raisins when there are no raisins with probability 0.2 and will incorrectly identify no raisins when there are raisins with probability 0.3. This decision network can be represented by the diagram below where \(E\) is her choice to eat, \(U\) is her utility earned, \(R\) is whether the cookie contains raisins, and \(S\) is her attempt at smelling.
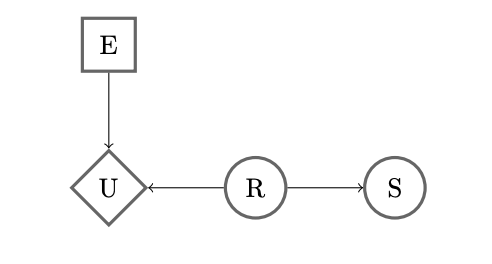
Valerie has just smelled the cookie and she thinks it doesn’t have raisins. Write the probability, \(X\), that the cookie has raisins given that she smelled no raisins as a simplest form fraction or decimal.
\[X = \]
Answer
\[X = 0.04\]
\[ P(+r|-s) = \frac{P(-s|+r)P(+r)}{P(-s)} = \frac{P(-s|+r)P(+r)}{P(-s|+r)P(+r)+P(-s|-r)P(-r)} = \frac{.3*.1}{.3*.1+.8*.9} = \frac{.03}{.75} = .04 \]36.2.3 (c)
What is her maximum expected utility, \(Y\) given that she smelled no raisins? You can answer in terms of \(X\) or as a simplest form fraction or decimal.
\[Y = \]
Answer
\[ Y = −100X + 10(1 − X), 5.6 \]
\[ \begin{aligned} MEU(-s) &= \max \big( MEU(\text{eating} \mid -s), \; MEU(\text{not eating} \mid -s) \big) \\ &= \max \big( P(+r \mid -s) \cdot EU(\text{eating}, +r) + P(-r \mid -s) \cdot EU(\text{eating}, -r), \; MEU(\text{not eating}) \big) \\ &= \max \big( X \cdot (-100) + (1 - X) \cdot 10, \; 0 \big) \\ &= X \cdot 100 + (1 - X) \cdot 10 \end{aligned} \]
36.2.4 (d)
What is the Value of Perfect Information (VPI) of smelling the cookie? You can answer in terms of \(X\) and \(Y\) or as a simplest form fraction or decimal.
\[ VPI = \]
Answer
\(VPI = 0.75 ∗ Y ,4.2\)
\(VPI(S) = MEU(S) - MEU(\varnothing)\)
\(MEU(S) = P(-s)\,MEU(-s) + P(+s)\,MEU(+s)\)
\(P(-s) = 0.75 \quad \text{(from part (c))}, \quad MEU(-s) = Y\)
\(MEU(+s) = 0\) because it was better for her to not eat the raisin without knowing anything. Smelling raisins will only make it more likely for the cookie to have raisins, and it will still be best for her to not eat and earn a utility of 0.
\(MEU(\varnothing) = 0\)
\(VPI(S) = 0.75 \cdot Y + 0 - 0 = 0.75 \cdot Y\)