34 Discussion 06: Probability and Bayes Nets (From Spring 2025)
Slides
34.1 Bayes’ Nets Representation and Probability
Suppose that a patient can have a symptom (\(S\)) that can be caused by two different, independent diseases (\(A\) and \(B\)). It is known that the variation of gene \(G\) plays a big role in the manifestation of disease \(A\). A model and some conditional probability tables for this situation are shown below. For each part, you may leave your answer as an arithmetic expression.

34.1.1 (a)
Compute the following entry from the joint distribution:
\[ P(+g, +a, +b, +s) = \]
Answer
\[ P(+g, +a, +b, +s) = P(+g)P(+a|+g)P(+b)P(+s|+b, +a) = (0.1)(1.0)(0.4)(1.0) = 0.04 \]34.1.2 (b)
What is the probability that a patient has disease \(A\)?
\[P(+a) = \]
Answer
\[ P(+a) = P(+a|+g)P(+g) + P(+a|−g)P(−g) = (1.0)(0.1) + (0.1)(0.9) = 0.19 \]34.1.3 (c)
What is the probability that a patient has disease \(A\) given that they have disease \(B\)?
\[ P(+a|+b) = \]
Answer
\[ P(+a|+b) = P(+a) = 0.19 \]
This equality holds true as we have \(A \perp\!\!\!\perp B\) which is given in the problem. You can also infer this from the graph of the Bayes’ net via d-separation, which is covered in future lectures.34.1.4 (d)
What is the probability that a patient has disease \(A\) given that they have symptom \(S\) and disease \(B\)?
Answer
\[ P(+a \mid +s, +b) = \frac{P(+a,+b,+s)}{P(+a,+b,+s)+P(-a,+b,+s)} = \frac{P(+a)P(+b)P(+s \mid +a,+b)}{P(+a)P(+b)P(+s \mid +a,+b)+P(-a)P(+b)P(+s \mid -a,+b)} \]
\[ = \frac{(0.19)(0.4)(1.0)}{(0.19)(0.4)(1.0)+(0.81)(0.4)(0.8)} = \frac{0.076}{0.076+0.2592} \approx 0.2267 \]34.1.5 (e)
What is the probability that a patient has the disease carrying gene variation \(G\) given that they have disease \(A\)?
\[ P(+g \mid +a) = \]
Answer
\[ P(+g | +a) = \frac{P(+g)P(+a|+g)}{P(+g)P(+a|+g) + P(-g)P(+a|-g)} = \frac{(0.1)(1.0)}{(0.1)(1.0) + (0.9)(0.1)} = \frac{0.1}{0.1+0.09} = 0.5263 \]34.1.6 (f)
What is the probability that a patient has the disease carrying gene variation \(G\) given that they have disease \(B\)?
\[ P(+g| +b) = \]
Answer
\[ P(+g| +b) = P(+g) = 0.1 \]
The first equality holds true as we have \(G \perp\!\!\!\perp B\), which can be inferred from the graph of the Bayes’ net.34.2 Bayes Nets: Representation
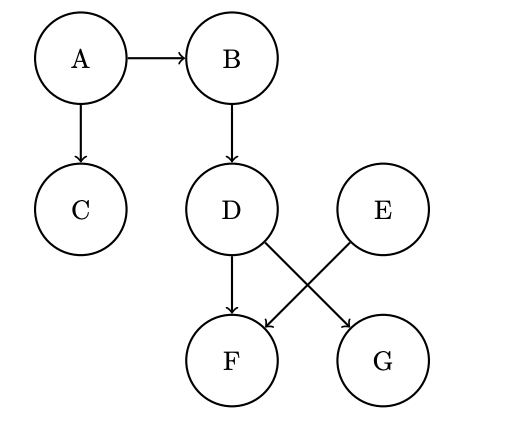
Parts (a), (b), and (c) pertain to the following Bayes’ Net.
34.2.1 (a)
Express the joint probability distribution as a product of terms from the Bayes Nets CPTs.
Answer
\[ P(A)P(C|A)P(B|A)P(D|B)P(E)P(F|D, E)P(G|D) \]34.2.2 (b)
Assume each node can take on 4 values. How many entries do the factors at \(A\), \(D\), and \(F\) have?
\(A:\) \(D:\) \(F:\)
Answer
\(A: 4\) \(D: 4^2\) \(F:4^3\)
34.2.3 (c)
Mark all that are guaranteed to be true:
Answer
Parts (d) and (e) pertain to the following CPTs.
| A | \(P(A)\) |
|---|---|
| +a | 0.8 |
| -a | 0.2 |
| A | B | \(P(B\|A)\) |
|---|---|---|
| +a | +b | 0.9 |
| +a | -b | 0.1 |
| -a | +b | 0.6 |
| -a | -b | 0.4 |
| B | C | \(P(C\|B)\) |
|---|---|---|
| +b | +c | 0.8 |
| +b | -c | 0.2 |
| -b | +c | 0.8 |
| -b | -c | 0.2 |
| C | D | \(P(D\|C)\) |
|---|---|---|
| +c | +d | 0.25 |
| +c | -d | 0.75 |
| -c | +d | 0.5 |
| -c | -d | 0.5 |
34.2.4 (d)
State all non-conditional independence assumptions that are implied by the probability distribution tables.
Answer
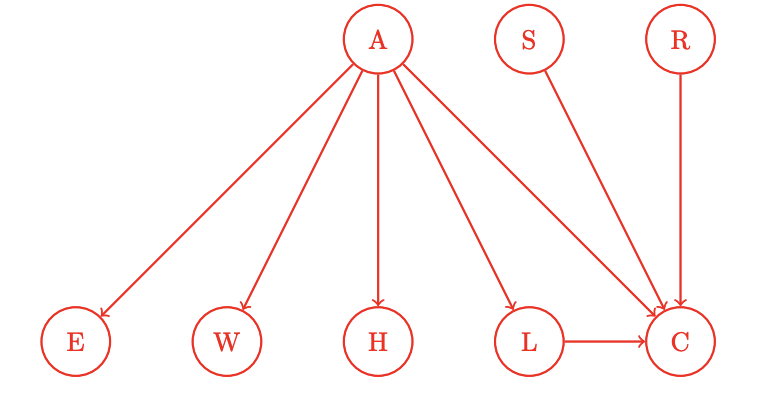
From the tables, we have \(A\not\!\perp\!\!\!\perp B \mid D\) and \(C\not\!\perp\!\!\!\perp B \mid D\), and \(B \perp\!\!\!\perp C\).You are building advanced safety features for cars that can warn a driver if they are falling asleep (\(A\)) and also calculate the probability of a crash (\(C\)) in real time. You have at your disposal 6 sensors (random variables):
\(E\): whether the driver’s eyes are open or closed
\(W\): whether the steering wheel is being touched or not
\(L\): whether the car is in the lane or not
\(S\): whether the car is speeding or not
\(H\): whether the driver’s heart rate is somewhat elevated or resting
\(R\): whether the car radar detects a close object or not
A influences {\(E\), \(W\), \(H\), \(L\), \(C\)}. \(C\) is influenced by {\(A\), \(S\), \(L\), \(R\)}.
34.2.5 (e)
Draw the Bayes Net associated with the description above by adding edges between the provided nodes where appropriate.
Answer