38 Discussion 10: ML I (From Spring 2025)
Slides
38.1 Perceptron
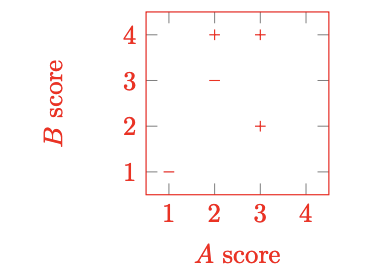
You want to predict if movies will be profitable based on their screenplays. You hire two critics A and B to read a script you have and rate it on a scale of 1 to 4. The critics are not perfect; here are five data points including the critics’ scores and the performance of the movie:
| # | Movie Name | A | B | Profit? |
|---|---|---|---|---|
| 1 | Pellet Power | 1 | 1 | - |
| 2 | Ghosts! | 3 | 2 | + |
| 3 | Pac is Bac | 2 | 4 | + |
| 4 | Not a Pizza | 3 | 4 | + |
| 5 | Endless Maze | 2 | 3 | - |
38.1.1 (a)
First, you would like to examine the linear separability of the data. Plot the data on the 2D plane above; label profitable movies with \(+\) and non-profitable movies with \(-\) and determine if the data are linearly separable.
Answer
The data are linearly separable.
38.1.2 (b)
Now you decide to use a perceptron to classify your data. Suppose you directly use the scores given above as features, together with a bias feature. That is \(f_0 = 1\), $f_1 = $ score given by A and $f_2 = $ score given by B.
Run one pass through the data with the perceptron algorithm, filling out the table below. Go through the data points in order, e.g. using data point #1 at step 1.
| step | Weights | Score | Correct? |
|---|---|---|---|
| 1 | |||
| 2 | |||
| 3 | |||
| 4 | |||
| 5 |
Answer
| step | Weights | Score | Correct? |
|---|---|---|---|
| 1 | [-1, 0, 0] | -1 ⋅ 1 + 0 ⋅ 1 + 0 ⋅ 1 = -1 | yes |
| 2 | [-1, 0, 0] | -1 ⋅ 1 + 0 ⋅ 3 + 0 ⋅ 2 = -1 | no |
| 3 | [0, 3, 2] | 0 ⋅ 1 + 3 ⋅ 2 + 2 ⋅ 4 = 14 | yes |
| 4 | [0, 3, 2] | 0 ⋅ 1 + 3 ⋅ 3 + 2 ⋅ 4 = 17 | yes |
| 5 | [0, 3, 2] | 0 ⋅ 1 + 3 ⋅ 2 + 2 ⋅ 3 = 12 | no |
38.1.3 (c)
Have weights been learned that separate the data?
Answer
With the current weights, points will be classified as positive if \(-1 \cdot 1 + 1\cdot A + -1 \cdot B \ge 0 \quad \text{or} \quad A - B \ge 1\). So we will have incorrect predictions for data points 3:
\[ -1 \cdot 1 + 1 \cdot 2 + -1 \cdot 4 = -3 < 0 \]
and 4:
\[ -1 \cdot 1 + 1 \cdot 3 + -1 \cdot 4 = -2 < 0 \]
Note that although point 2 has \(w \cdot f = 0\), it will be classified as positive (since we classify as positive if \(w \cdot f \ge 0\)).38.1.4 (d)
More generally, irrespective of the training data, you want to know if your features are powerful enough to allow you to handle a range of scenarios. Circle the scenarios for which a perceptron using the features above can indeed perfectly classify movies which are profitable according to the given rules:
38.1.4.1 (i)
Your reviewers are awesome: if the total of their scores is more than 8, then the movie will definitely be profitable, and otherwise it won’t.
Answer
Can classify (consider weights [-8, 1, 1])38.1.4.2 (ii)
Your reviewers are art critics. Your movie will be profitable if and only if each reviewer gives either a score of 2 or a score of 3.
Answer
Cannot classify38.1.4.3 (iii)
Your reviewers have weird but different tastes. Your movie will be profitable if and only if both reviewers agree.
Answer
Cannot classify38.2 Neural Network Representations
You are given a number of functions (a-h) of a single variable, \(x\), which are graphed below.
The computation graphs on the following pages will start off simple and get more complex, building up to neural networks. For each computation graph, indicate which of the functions below they are able to represent.

(a) \(2x\)

(b) \(4x - 5\)
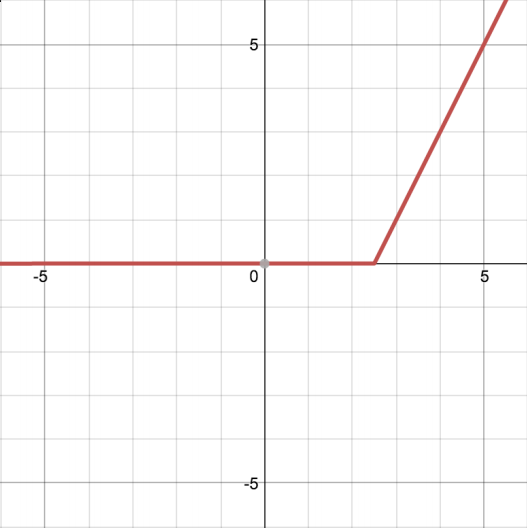
(c) \[\begin{cases} 2x - 5 & x \ge 2.5 \\ 0 & x < 2.5 \end{cases}\]
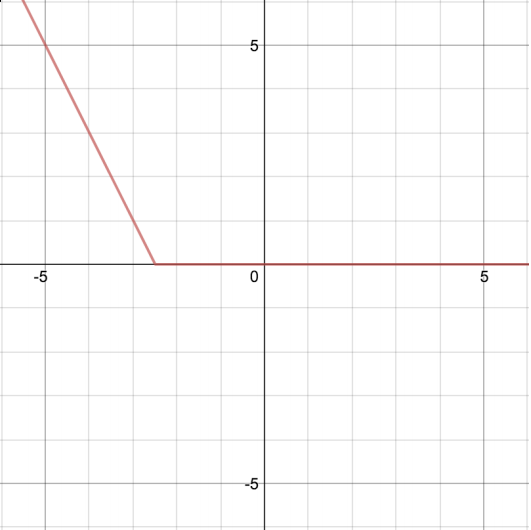
(d) \[\begin{cases} -2x - 5 & x \le -2.5 \\ 0 & x > -2.5 \end{cases}\]
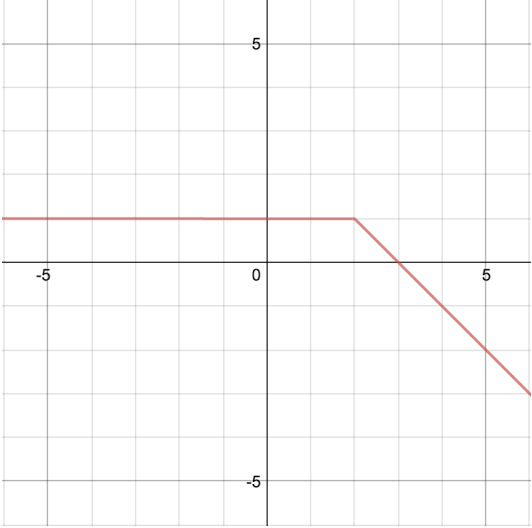
(e) \[\begin{cases} -x + 3 & x \ge 2 \\ 1 & x < 2 \end{cases}\]
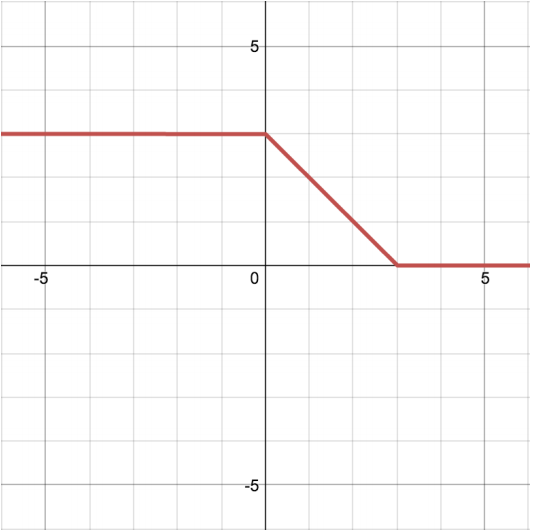
(f) \[\begin{cases} 3 & x \le 0 \\ 3 - x & 0 < x \le 3 \\ 0 & x > 3 \end{cases}\]

(g) \(log(x)\)
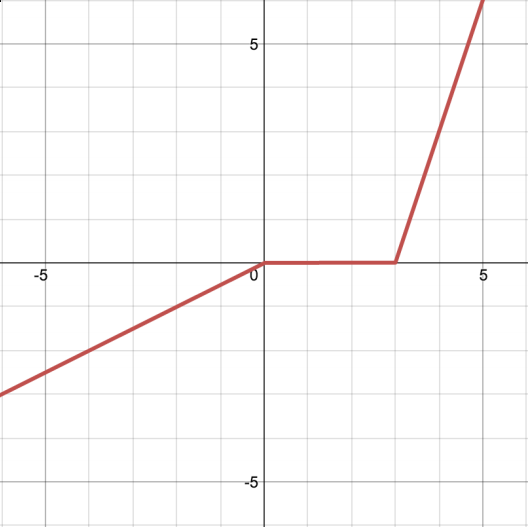
(h) \[\begin{cases} 0.5 x & x \le 0 \\ 0 & 0 < x \le 3 \\ 3x - 9 & x > 3 \end{cases}\]
38.2.1 (a)
Consider the following computation graph, computing a linear transformation with scalar input \(x\), weight \(w\), and output \(o\), such that \(o = wx\). Which of the functions can be represented by this graph? For the options which can, write out the appropriate value of \(w\).

Answer
This graph can only represent (a), with \(w = 2\). Since there is no bias term, the line must pass through the origin.38.2.2 (b)
Now we introduce a bias term \(b\) into the graph, such that \(o = wx + b\) (this is known as an affine function). Which of the functions can be represented by this network? For the options which can, write out an appropriate value of \(w, b\).

Answer
(a) with \(w = 2\) and \(b = 0\), and (b) with \(w = 4\) and \(b = -5\).38.2.3 (c)
We can introduce a non-linearity into the network as indicated below. We use the ReLU non-linearity, which has the form \(ReLU(x) = \max(0, x)\). Now which of the functions can be represented by this neural network with weight \(w\) and bias \(b\)? For the options which can, write out an appropriate value of \(w, b\).

Answer
With the output coming directly from the ReLU, this cannot produce any values less than zero.It can produce (c) with \(w = 2\) and \(b = -5\), and (d) with \(w = -2\) and \(b = -5\).
38.2.4 (d)
Now we consider neural networks with multiple affine transformations, as indicated below. We now have two sets of weights and biases \(w_1, b_1\) and \(w_2, b_2\). We denote the result of the first transformation \(h\) such that \(h = w_1 x + b_1\), and \(o = w_2 h + b_2\). Which of the functions can be represented by this network? For the options which can, write out appropriate values of \(w_1, w_2, b_1, b_2\).

Answer
Applying multiple affine transformations (with no non-linearity in between) is not any more powerful than a single affine function: \(w_2(w_1 x + b_1) + b_2 = w_2 w_1 x + w_2 b_1 + b_2\), so this is just a single affine function with different coefficients.The functions we can represent are the same as in (b):
(a) with \(w_1 = 2, w_2 = 1, b_1 = 0, b_2 = 0\), and (b) with \(w_1 = 4, w_2 = 1, b_1 = 0, b_2 = -5\).
38.2.5 (e)
Next we add a ReLU non-linearity to the network after the first affine transformation, creating a hidden layer. Which of the functions can be represented by this network? For the options which can, write out appropriate values of \(w_1, w_2, b_1, b_2\).

Answer
(c), (d), and (e).
The affine transformation after the ReLU is capable of stretching (or flipping) and shifting the ReLU output in the vertical dimension.
- (c) \(w_1 = 2, b_1 = -5, w_2 = 1, b_2 = 0\)
- (d) \(w_1 = -2, b_1 = -5, w_2 = 1, b_2 = 0\)
- (e) \(w_1 = 1, b_1 = -2, w_2 = -1, b_2 = 1\)
38.2.6 (f)
Now we add another hidden layer to the network, as indicated below. Which of the functions can be represented by this network?

Answer
(c), (d), (e), and (f).The network can represent all the same functions as (e). In addition it can represent (f): the first ReLU produces the first flat segment, the affine transformation can flip and shift the curve, and the second ReLU produces the second flat segment.
(h) cannot be produced since its line has only one flat segment; the affine layers can only scale, shift, and flip in the vertical dimension.
38.2.7 (g)
We’d like to consider using a neural net with just one hidden layer, but have it be larger—a hidden layer of size 2. Let’s first consider using just two affine functions, with no nonlinearity in between. Which of the functions can be represented by this network?

Answer
(a) and (b). With no non-linearity, this reduces to a single affine function.38.2.8 (h)
Now we’ll add a non-linearity between the two affine layers, to produce the neural network below with a hidden layer of size 2. Which of the functions can be represented by this network?

Answer
All functions except (g).We can recreate any network from (e) by setting \(w_4 = 0\), producing (c), (d), and (e).
To produce the rest: \(h_1'\) and \(h_2'\) are two independent ReLU outputs, each with a flat part on the x-axis and a positive slope portion.
The final layer takes a weighted sum of these two functions.
- (a) and (b): flat portion of one ReLU starts where the other ends; final layer flips/combines to produce a sloped line.
- (f): both ReLUs have equal slope, canceling to produce the first flat portion above the x-axis.
- (h): down-sloping ReLU flat portion ends before the other’s flat portion begins; combining produces the correct shape.
